セルシウス温度とは,「1気圧のもとで氷がとける温度を0℃,水が沸騰する温度を100℃」と定めた温度です。 これは日常生活をしていくうえで,便宜的に決められた温度です。 これに対して, 絶対温度とは,「原子・分子の熱運動がほとんどなくなる温度を0k」とする温度です。分子が長いので、ミクロ的にみると、部分部分の分 子はまだある程度の運動を行うことができる。(ミクロ ブラウン運動)ゴム状態。 ガラス転移温度以下まで温度を下げると、分子鎖 の部分的な運動性も失われて、ゴムから柔軟性 は失われる。この状態光速が速度の上限だから、分子が全部光速で運動したら、それが最高温度。 というものだ。高校物理の範囲でも1/2mv ^2 = 3/2kTという式は出てくるので、1/2mc ^2 = 3/2kTとなるT(cは光速度)が最高温度だ、というわけである。
Adoko 熱力学 気体の熱力学
温度とは 分子運動
温度とは 分子運動-熱力学温度のケルビン(k)とは、分子の運動が止まった状態 (実際には完全に止まることはありませんが)の温度を 0(ゼロ) kとしたものです。 熱のエネルギー 今月のまめ知識 第23回金属とは温度と運動エネルギーの関係をもう少し詳しくみていきましょう。 水分子一つ一つの質量をm、速さをvとおくと、水分子の運動エネルギーは1/2・mv 2 ですね。 この運動エネルギーと絶対温度T Kの間には、実は 比例関係 があります。




温度と分子運動 Npo法人 楽知ん研究所
気体分子の運動エネルギー 1個の分子の運動エネルギー E= 1 2 mv2 平均の運動エネルギーは、 「v2 の平均値」を表す式 「根平均二乗速さ」の二乗 平均の運動エネルギーは ・絶対温度に比例 ・分子の種類に無関係 = 1 2 mv2F s (v)dv 0 "!温度と反応速度 DongJoon 分子運動(ぶんしうんどう) シミュレーション, 熱(ねつ) シミュレーション 熱と分子運動 すべての物体は目で見ることができない原子や分子で空気の分子が飛び回って衝突し,跳ね返る様子が実に 良く表されています。現在,ダウンロード販売中ですので,詳細は, 小林さん(GCD@niftynejp)までお問い合わせください。 また杉浦裕文さんの『仮説実験授業ノート 温度と分子運動』(ガ
固体中の分子は移動はしていませんが振動していて、温度が高いほど大きな(激しい)振動をします。 つまり、分子の振動エネルギーや運動エネルギーの大小が温度の高低なのです。また、熱は分子の動き により発生する運動エネルギー ということです。2固 相重合における分子運動 分子の運動と反応との関係が比較的明りょうに示され ているのは固相重合においてであろう。 固相におけるモノマーの分子運動は多くの外的条件に よって規鯛される。すなわち温度,圧 力,添 加物などに よって,固 相における ガラス転移点とミクロブラウン運動 非晶性部分を持つ高分子は、ゴム状態という液体と固体の中間のような状態があり、ガラス転移点よりも低温になると固まる、ということがわかりました。 でもなぜ、このような現象が起こるのでしょうか。 それには
度に応じて分子の形態やパッキングが変化する必要がある。 しかし,温度低下に伴って分子運動性が低下すると,やが て分子形態およびパッキングの変化が温度低下に追いつけ なくなり,系は非平衡状態になる。80℃付近のポリスチレ気体分子運動論(きたいぶんしうんどうろん、英語 kinetic theory of gases )は、原子論の立場から気体を構成する分子の運動を論じて、その気体の巨視的性質や行動を探求する理論である。 気体運動論や分子運動論とも呼ばれる。最初は単一速度の分子群のモデルを使ってボイルの法則の説明をし3 199 1 東京電機大学工学部物理系列(〒1 8551 東京都足立区千住 旭町5 番) Vol 56, No 6, 13 ―()― 講座 気体分子運動論の基礎 松 田 七美男 1 Basic Concepts to Kinetic Theory of Gases




センター18物理第1問 問4 気体分子の平均運動エネルギーと2乗平均速度 理科が好き Com




45 分子の平均運動エネルギーと絶対温度 Youtube
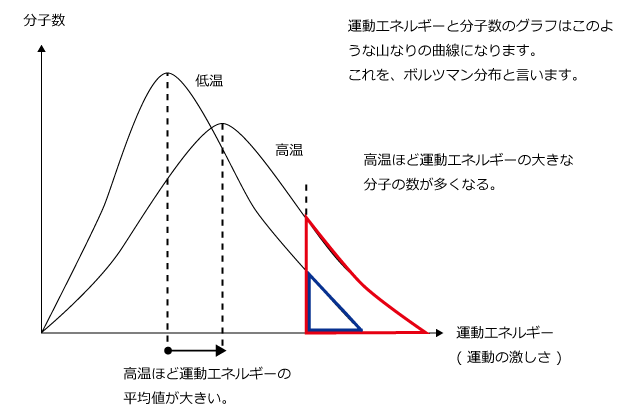
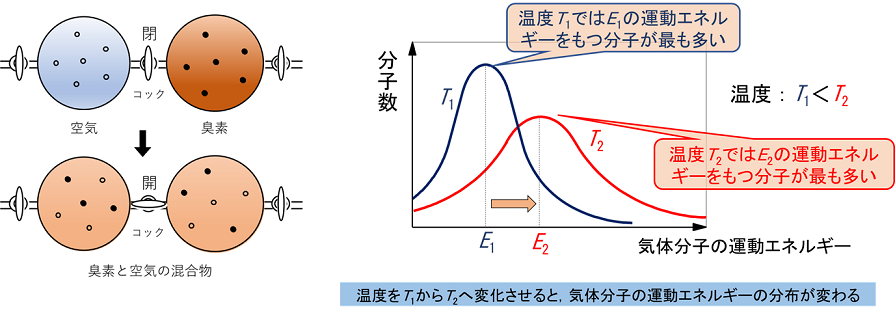
温度が高くなると、運動エネルギーが大きい粒子が増加し、平均値が高くなっている のが確認できるね。 まとめ 最後に、この『グラフ温度と分子の運動エネルギーの関係を図を使って解説!』のページで解説した内容をまとめておく。温度は分子集団の状態(平均運動エネ ルギー)ですが、熱は集団から集団へ移動するエネルギーの量です。 理想気体の圧力 2圧力は面積当たりの力で、その単位はN/m で、Paとも書きます。この節の説明を気体の分 子運動論といい「気体の圧力は、多くの気体分2原子分子は、分子の並進運動だけでなく 分子の空間的な運動(回転運動、振動運動)のような分子内部構造 も熱力学的な性質(比熱など・・・)に影響を与えます。 今、2原子分子の原子間の相互作用(バネのような相互作用ポテンシャル)は考えますが



冷凍講座 温度の話 前川製作所 技術研究所 R D Center




問100 92 解説 Yaku Tik 薬学まとめました
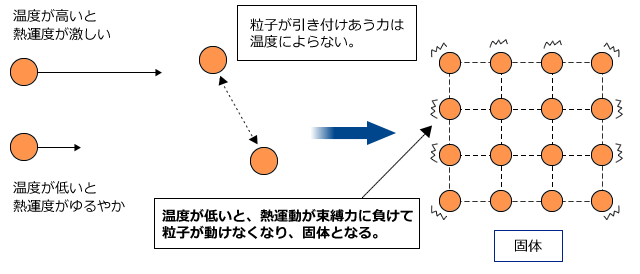
つまり、気体中の分子の運動エネルギーは温度に比例する、逆に言えば気体の温度というのは分子の運動エネルギーに対応していることを意味する。 ここで出てきた比例定数 kB はボルツマン定数と呼ばれる定数であり である。 分子1個あたりの持つ運動この式を発展させると,ボイルの法則になる。 分子の運動と固体・液体・気体の状態 (1) 固体 温度が下がって粒子の運動エネルギーが小さくなり,粒子間に働く結合力で粒子が規則正しく密に並んだ状態。 したがって,一定の形,体積をもつ。この状態で粒子が行う運動は,一定位置を中心に熱と温度の基本的な違いはわずかですが重要です。熱は分子運動の全体的なエネルギーですが、温度は分子運動の平均的なエ ネルギーです。 それでは、以下の記事を見てみましょう。ここでは、2つを単純化しました。 比較表



音速の理論2 分子速度と比熱比
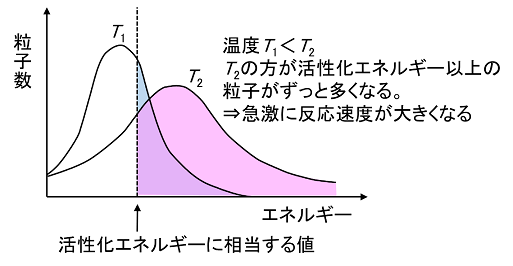



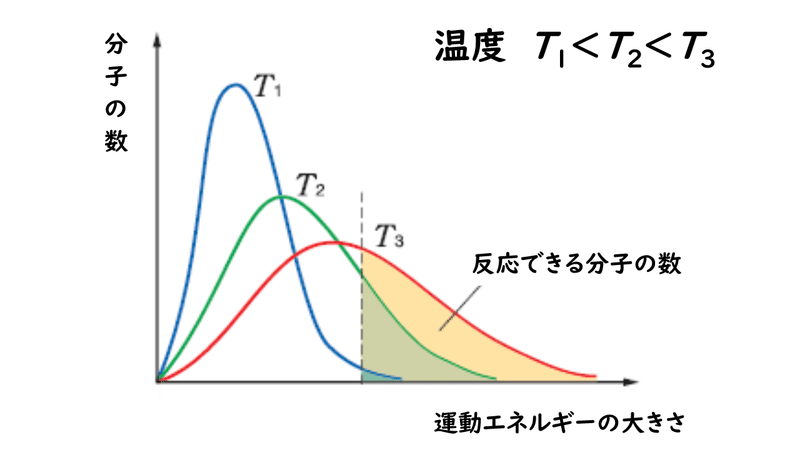
反応条件と反応速度
液体の中では多数の分子がさまざまな速度ででたらめな方向に運動しています。ここでは分子の速度の分布が温度で決まることを元に、液体のいくつかの性質を考えます。 31 分子の速度分布 ―― マク温度tは に関係していることを示している。 気体分子運動論は,クラジウス,ベルヌーイ,マックスウエル,ボルツマンらによって考えられた。 12-4 分子の平均運動エネルギーと絶対温度気体の分子運動の考察からボイルの法則を導く ・ より となり,温度一定では分子の平均速度 も 一定となるので, は一定(ボイルの法則) 2 3 1 pV Nmc c pV 実験をしなくても思考実験で導けた! V




高校物理 絶対温度と分子の運動エネルギー 映像授業のtry It トライイット
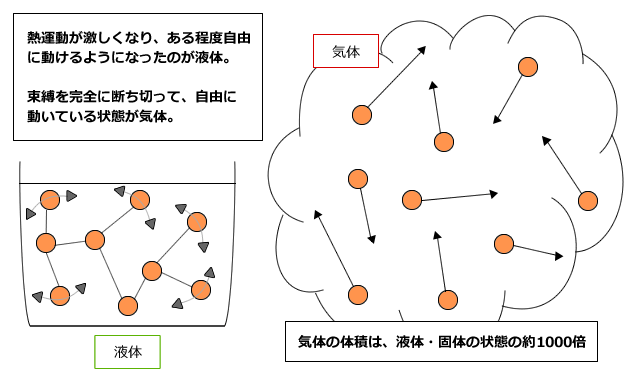



化学講座 第31回 熱化学方程式 状態変化と熱の出入り 私立 国公立大学医学部に入ろう ドットコム
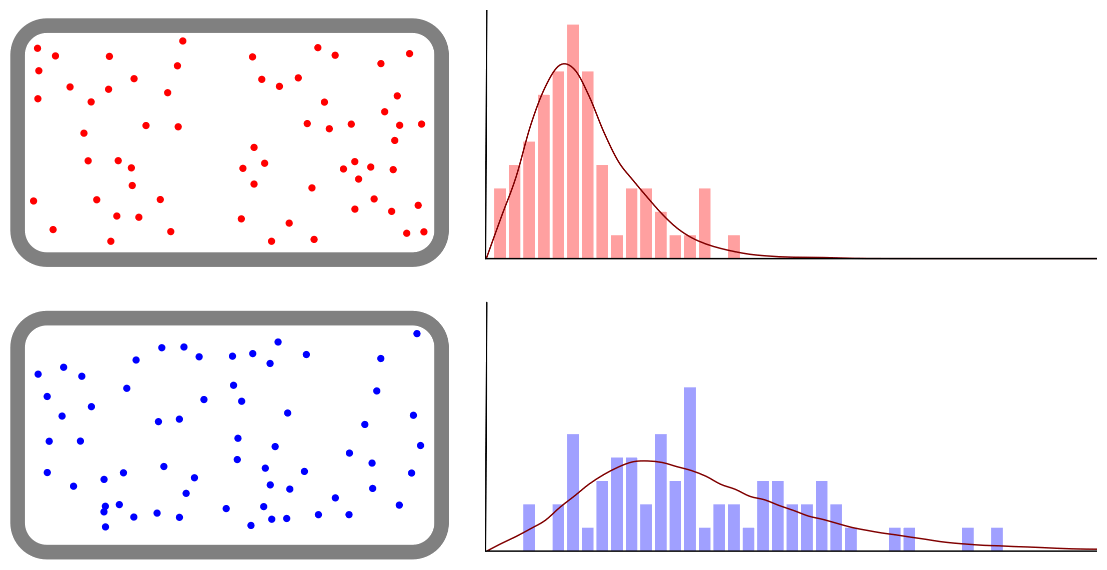
= 1 2 mv2 E= 1 2 mv2F s (v)dv 0 "! 逆に、分子運動が遅いほど、温度が低くなります。このように、温度は、分子運動の活発な程度を示した物理量です。 温度による粒子の速度分布グラフ 温度が低い気体は速力が遅い方に集中的に分布します。 気体の温度が高くなるほど、グラフは、横にノブナガ 「温度を下げるには、分子運動の激しさを小さくすればいいんじゃないかな? 母 「なら、分子運動の激しさを小さくするにはどうすれ



化学 気体分子の熱運動 技術情報館 Sekigin 気体の圧力を理解するため 気体分子の熱運動と分子の速度分布 マクスウェル分布 を紹介



化学講座 第38回 飽和蒸気圧 私立 国公立大学医学部に入ろう ドットコム
さきほど「温度は分子運動の激しさ」としましたが,もう少し詳しく言うと 「温度とは分子の運動エネルギーの平均値」と定義します。 空気中に分子はたくさん存在しており,それぞれの速さはいろいろで, その運動エネルギーもいろいろですが,それらマクスウェル速度分布からは,分子速度のピーク ν max = ( 2 k T / m ) 1/2 ,平均速度ν ave = ( 4 / π) 1/2 ν max となる。 なお,気体分子運動論における理想気体の単原子分子の二乗平均速度〈ν 2 〉= 3 k T / m となる。 衝突( collision ) 運動している 2 つの物体が接触し,短時間に力を相互に及ぼし温度が上がるにつれ、次第に振動運動が大きくなるようにになり、十分高い温度では 1 自由度あたり 熱容量に が加えられます。
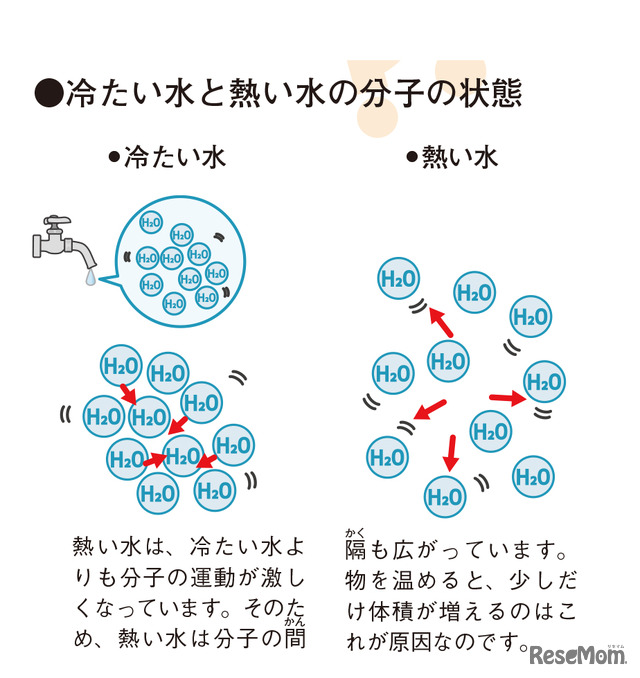



自由研究 物理 熱の正体にせまる 振動で水の温度を上げよう 中学生向け リセマム



Www Lasti U Hyogo Ac Jp Beam Physics Beamphysics Lecture Thermodynamics 2 Pdf
体分子の熱運動という.気体の熱運動は温度が高いほど,分子 量が小さいほど,運動の速度は速い. 圧力は国際単位系(SI)では, で表される.一方,大気の圧力を考える時は,直 気体分子運動論で考えると、当初の疑問は、払拭された・・・・という気持ちにさせてくれる(笑) 圧力は、 多数の粒子が動き回って、ポカポカ壁に激突したときの単位面積当たりの力 温度は、 粒子の平均の運動エネルギーと関連付けられる量個(多量)の分子はさまざまな方向に 運動していて,特定の方向に偏っていないとすると,平均的 には x , y , z 方向に運動する分子の数は等しいので, x 方向に運動する分子の数は それぞれの分子の速度の 2乗の平均値を と書くことにすると, これ



Http Honda Sci Yokohama Cu Ac Jp E5 8c 96 E5 Ad A6 E6 A6 E8 Acc 2 E7 Ab A0p Pdf
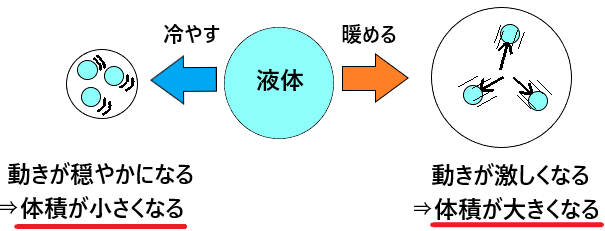



液体の膨張と圧縮とは 温度によって液体の体積が変化する仕組みを図解
2.分子運動論 まず目標は「温度を力学の言葉で書く」です(力学で使われる文字で書くということ)。 仮定は,一辺がLの立方体のなかに,質量mの分子がN個閉じ込められており, 分子と壁は完全弾性衝突する。この気体は理想気体の状態方程式に従う。




高校物理 コツコツと式変形 平均運動エネルギーと2乗平均速度 熱力学 お茶処やまと屋
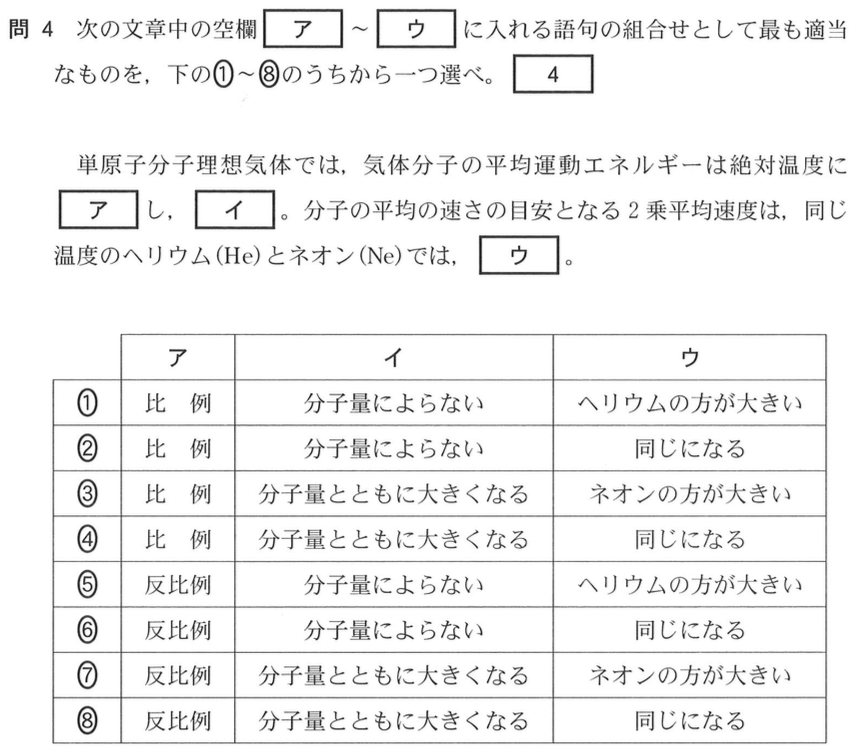



センター18物理第1問 問4 気体分子の平均運動エネルギーと2乗平均速度 理科が好き Com



なんとなくわかる高校化学 状態図




このグラフの見方を教えてください 温度が高いほど熱運動が大きくなるというのは分かって Clear




分子の運動エネルギーには並進の他に回転と振動があるということでしたが どういうことですか Shinshu Univ Physical Chemistry Lab Adsorption Group




物理がカンタンに 熱 気体分子の運動 Jtajdtnwのブログ




温度と分子運動 Npo法人 楽知ん研究所




内部エネルギーと温度 高校物理をあきらめる前に 高校物理をあきらめる前に



熱とエネルギー セルシウス温度と絶対温度ってなんですか 物理基礎 定期テスト対策サイト



化学 気体の性質と分子運動論 技術情報館 Sekigin 実在気体の特性 膨張 圧縮 拡大 拡散 濃度勾配 圧力 体積と温度の関係など を気体 分子運動論で扱う際の基本的な考え方を紹介
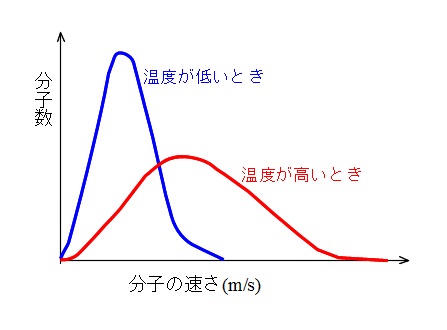



気体分子の熱運動と圧力の単位pa パスカル と大気圧



熱運動 わかりやすい高校物理の部屋
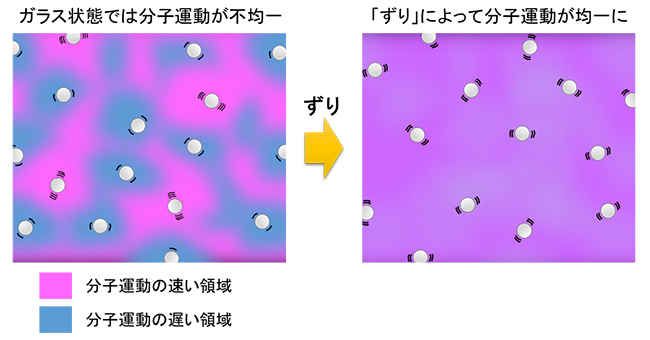



ガラス状態における分子運動の不均一性を ずり で解消 理化学研究所



化学講座 第31回 熱化学方程式 状態変化と熱の出入り 私立 国公立大学医学部に入ろう ドットコム
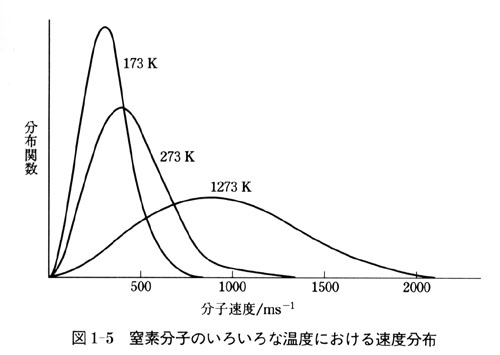



Info Ouj Ac Jp Hamada Textlib Rm Chap1 Figure
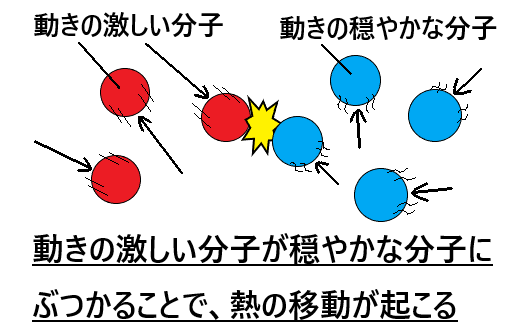



温度とは何か 物体の状態変化と温度の関係について解説
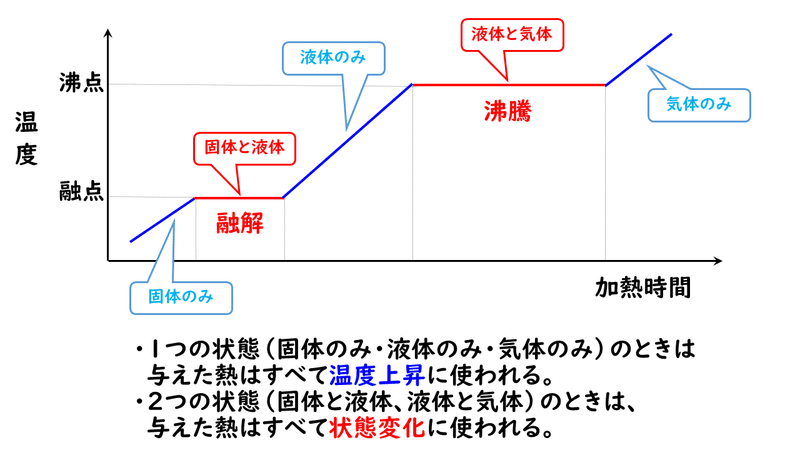



2 4 物質の三態と熱運動 おのれー Note




エントロピーが 時を戻す悪魔 を倒すまでの150年におよぶ戦い 高水 裕一 ブルーバックス 講談社 3 4
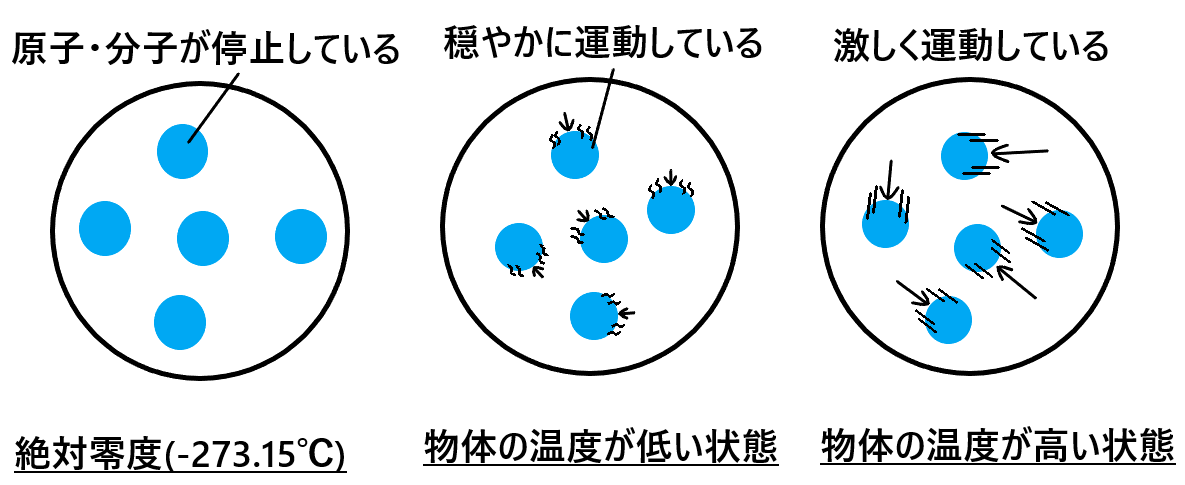



絶対零度とは また絶対零度の温度は何度なのか
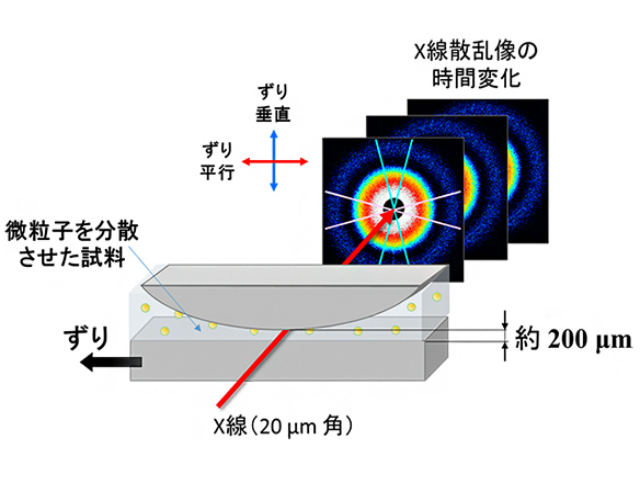



理研 ガラス状態の分子運動不均一性の解消を観測 Optronics Online オプトロニクスオンライン




高校物理 熱力学 02 B 気体分子の運動エネルギーと絶対温度 物理のしっぽ Youtube




気体分子運動11 温度その2 自然冷媒 水 のエアコンを創る



Adoko 熱力学 気体の熱力学
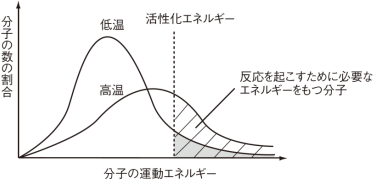



反応速度 高温で反応速度が大きくなるのはなぜですか 化学 定期テスト対策サイト



1



1




温度 Wikipedia




高校物理 絶対温度と分子の運動エネルギー 映像授業のtry It トライイット




高校化学基礎 熱運動と物質の状態 映像授業のtry It トライイット



温度と反応速度 Java実験室



化学 気体の性質と分子運動論 技術情報館 Sekigin 実在気体の特性 膨張 圧縮 拡大 拡散 濃度勾配 圧力 体積と温度の関係など を気体 分子運動論で扱う際の基本的な考え方を紹介
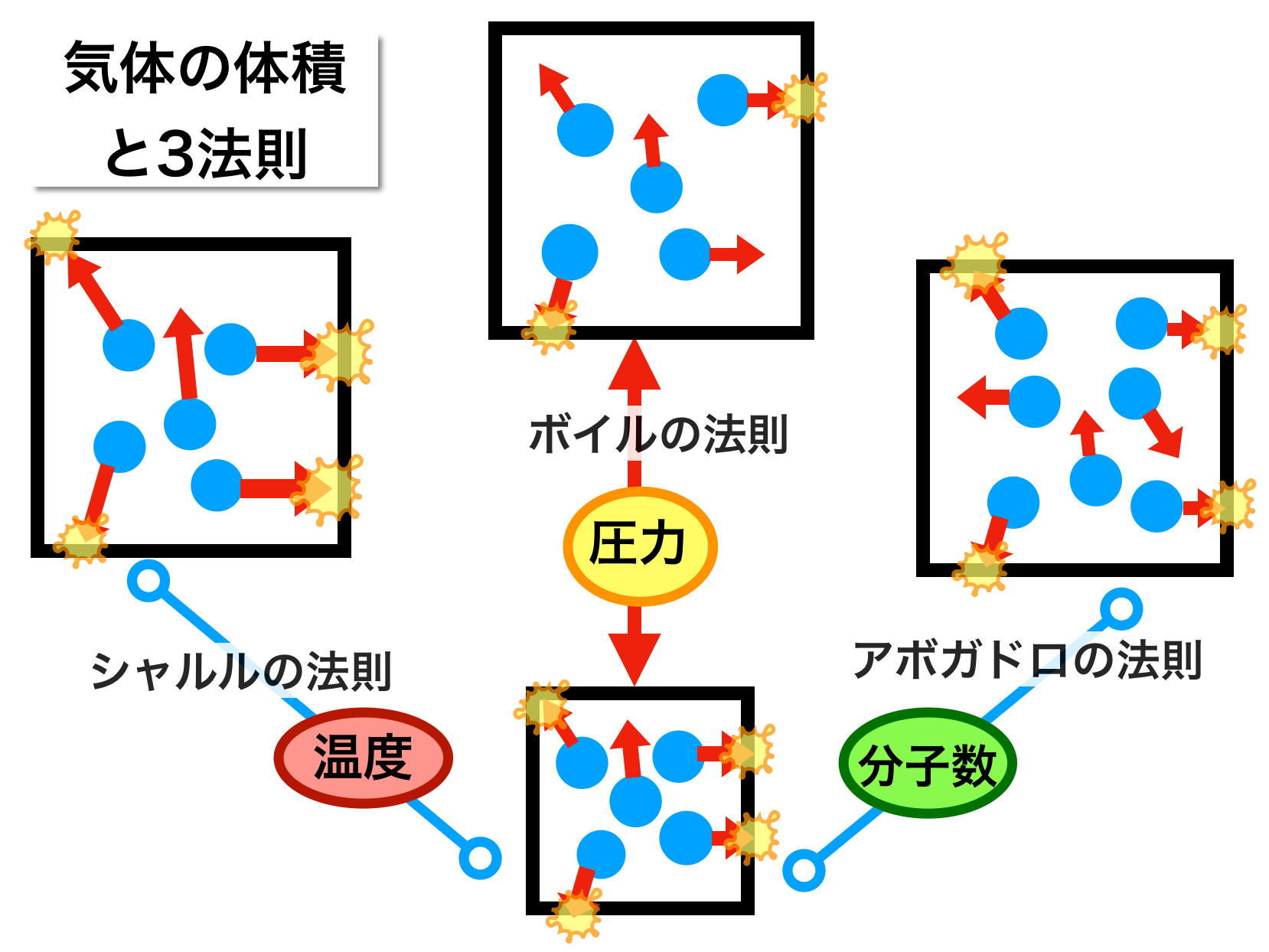



気体分子と体積の関係 ボイル シャルルの法則とアボガドロの法則 色と形で気象予報士
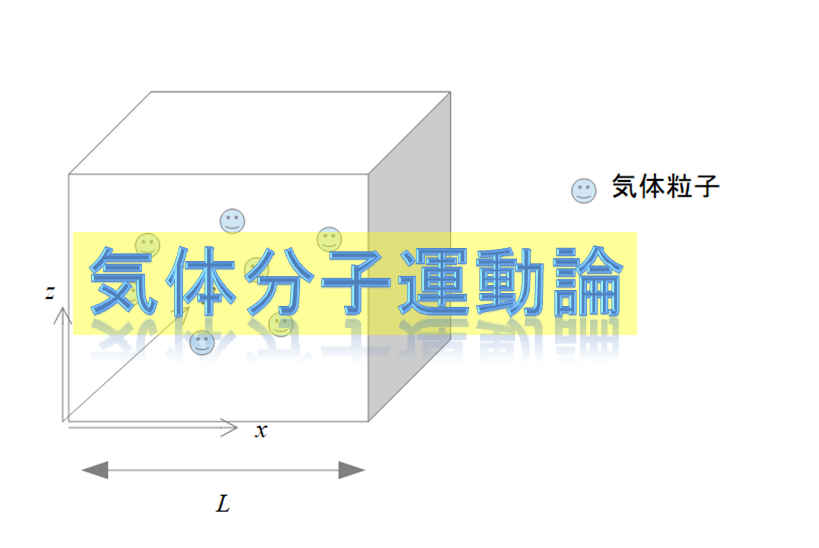



気体分子運動論 宇宙に入ったカマキリ



化学の分子のエネルギー分布曲線と温度についての質問です Yahoo 知恵袋




内部エネルギーの公式と求め方 理系ラボ



Www1 Doshisha Ac Jp Bukka Lecture Thermodyn Resume T Pca 12 02 Pdf




マナ物理 気体の分子運動論 再び 添付ファイル 4枚 を解いてください 気体の分子運動論 っぽいですが 通常の議論の展開ではないです 温度が気体分子1個の平均運動エネルギーを用いて定義されていて それを基にして解いていきます 内部



気体分子の運動
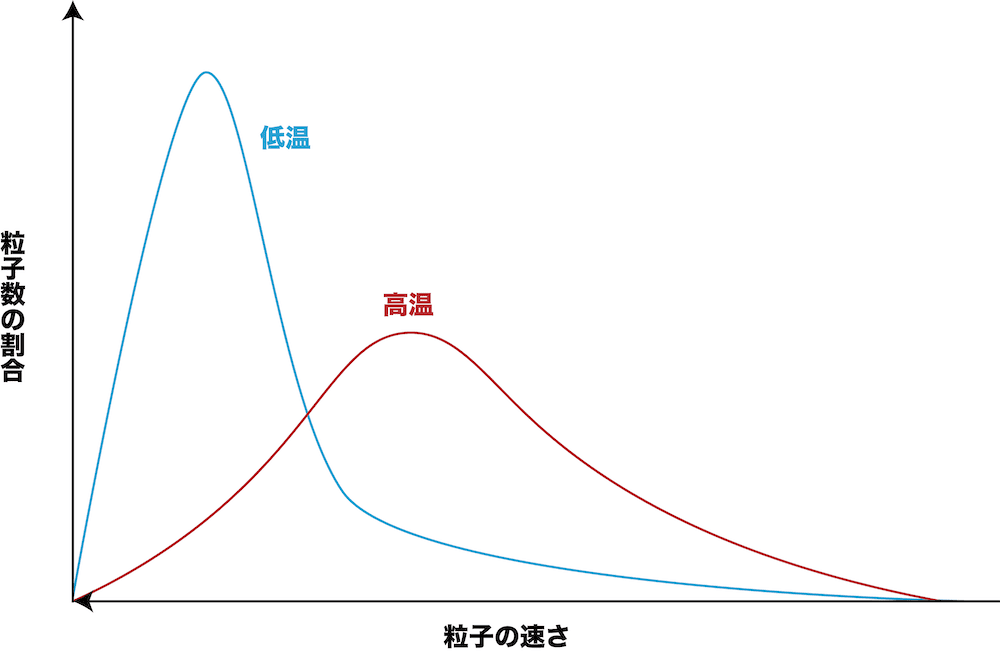



グラフ 温度と分子の運動エネルギーの関係を図を使って解説 化学のグルメ



粒子の熱運動



Adoko 熱力学 気体の熱力学



2 4 物質の三態と熱運動 おのれー Note




理想気体の比熱の温度依存性 5 2原子分子の回転の運動にもエネルギーが等分配されているのか 宇宙に入ったカマキリ




高校物理 熱力学11 気体の分子運動論 穴埋め問題で聞かれるポイント重視での説明 Youtube



温度とは
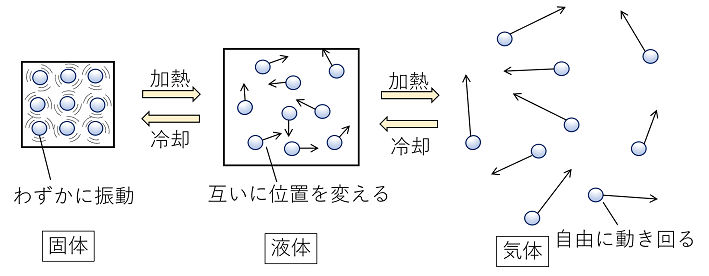



物質の三態と状態変化




高校物理 絶対温度と分子の運動エネルギー 映像授業のtry It トライイット



1



絶対零度 0 K




マナ物理 気体の分子運動論 再び 添付ファイル 4枚 を解いてください 気体の分子運動論 っぽいですが 通常の議論の展開ではないです 温度が気体分子1個の平均運動エネルギーを用いて定義されていて それを基にして解いていきます 内部
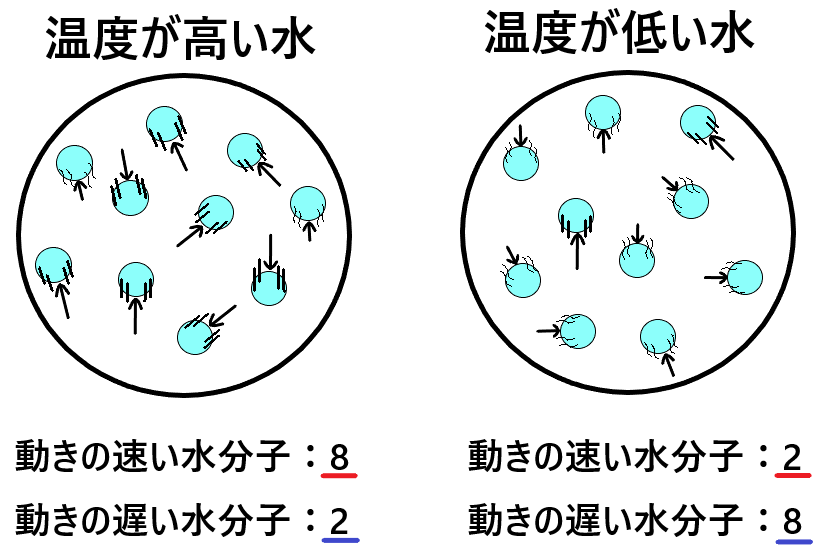



水が100度に達していないのに蒸発する仕組みとは



1 2 1 物質の状態と粒子の熱運動




薬剤師国家試験 医師国家試験 臨床 Ar Twitter マクスウェル ボルツマン分布 同じ温度でも気体分子のもつ分子運動エネルギーや速さにはバラツキがあります 図は 化学の基本ノート より Http T Co Dv5t0blwo8
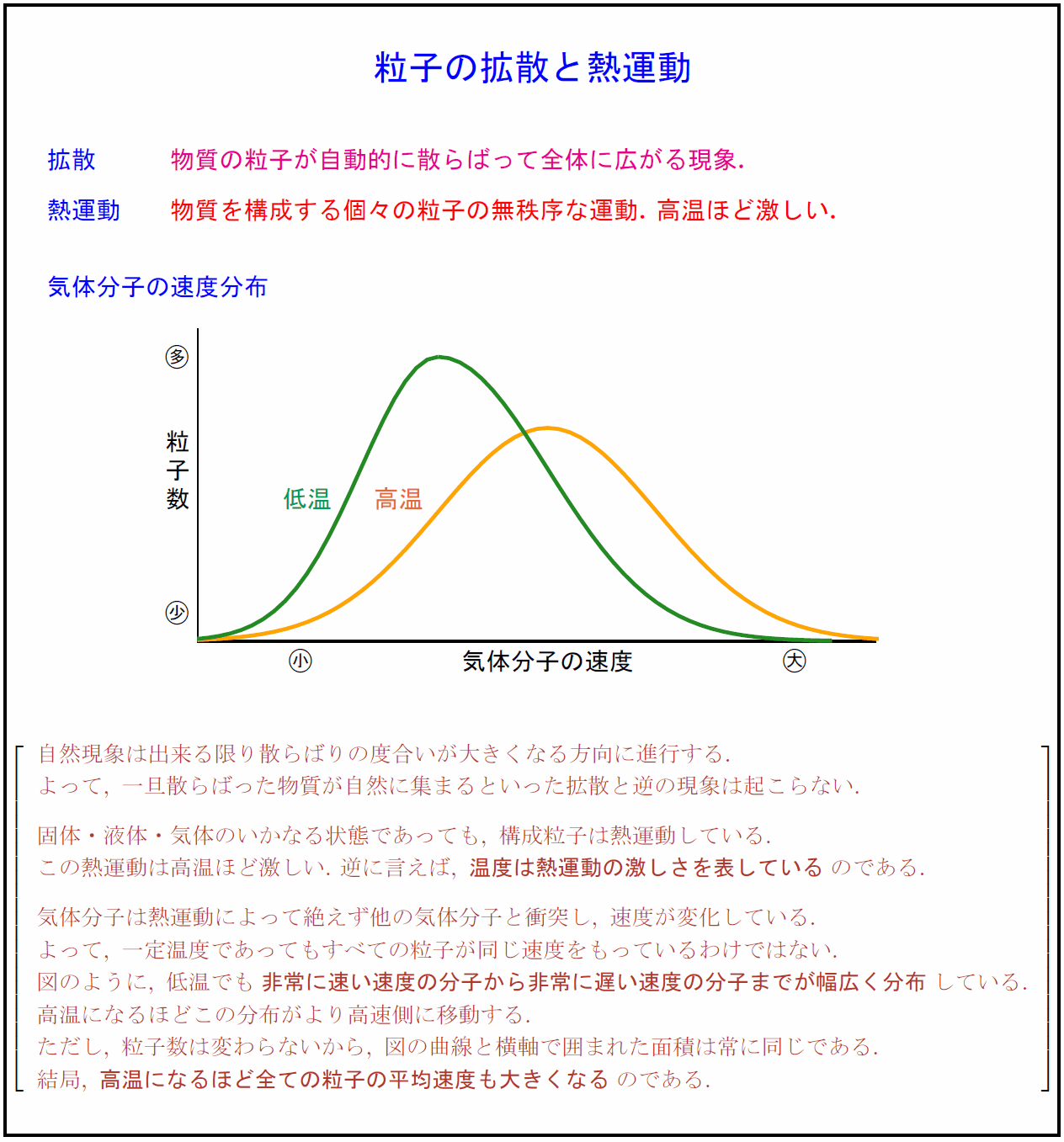



高校理論化学 粒子の拡散と熱運動 気体分子の速度分布 受験の月




物理 第4章熱力学ii Vol 4 1 2 B 分子のエネルギーと二乗平均速度 Youtube




気体分子運動11 温度その1 自然冷媒 水 のエアコンを創る



熱運動 わかりやすい高校物理の部屋




3 で質問です なぜ 1 16になるのですか 教えてください Clear




気体分子の速さについてなのですが 温度が高くなると 速さの大きい分子の数の割合は大き Clear
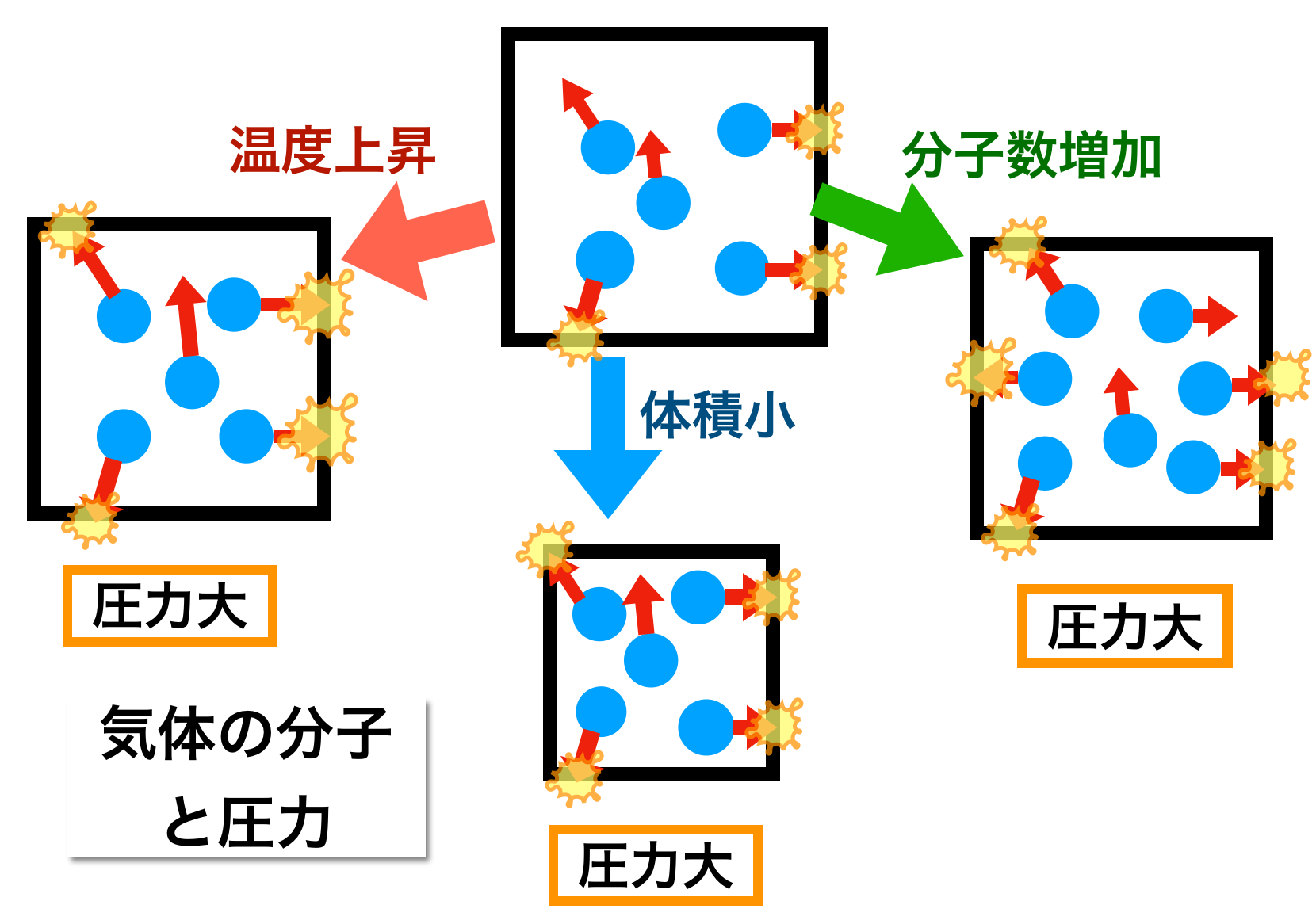



気体分子と圧力の関係 色と形で気象予報士




熱運動 と温度の関係を元塾講師がわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン




Ac Lihat Cara Penyelesaian Di Qanda




超低温物理学への招待




分子速度の求め方や温度との関係性 分子速度の計算




気体分子運動論 はどんな理論 理系学生ライターがわかりやすく解説 Study Z ドラゴン桜と学ぶwebマガジン



3 4 気体分子運動論と分子の運動 スペクトル色々




仮説社 Online Shop 授業ノート 温度と分子運動




高校物理 熱の現象も粒子の運動 温度と熱 熱力学 お茶処やまと屋



気体分子運動論とは 問題必勝パターンを分かりやすく解説 受験物理 Set Up
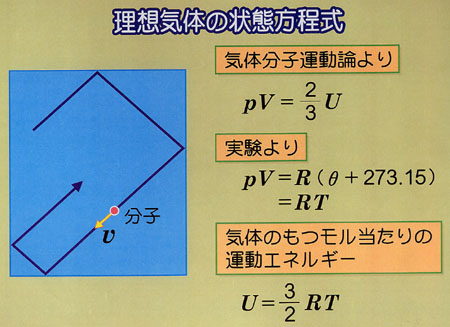



2 温度 気体の中では 分子は自由に飛び廻っており 理想気体の条件下で その運動エネルギーは絶対温度に比例することが実験で示された この場合 セルシウス A Celsius 温度8 1 Atmにおける水の氷点をo 沸点を100 とする温度目盛 で
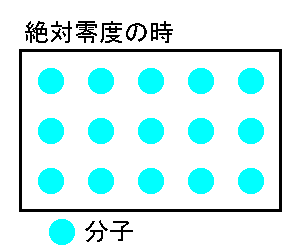



絶対温度について
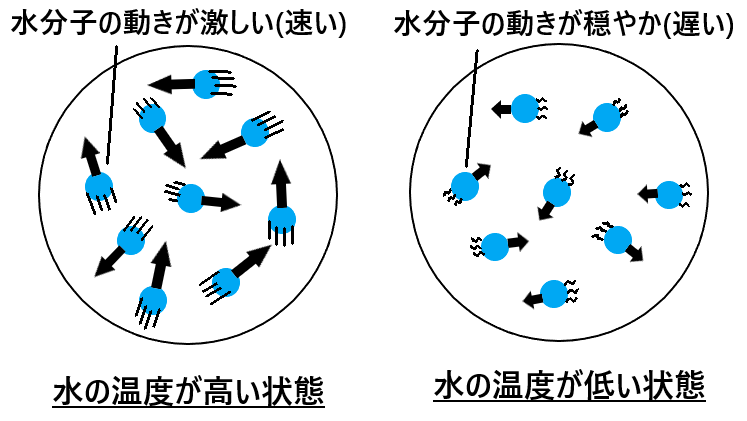



温度とは何か 物体の状態変化と温度の関係について解説




マナ物理 気体の分子運動論 再び 添付ファイル 4枚 を解いてください 気体の分子運動論 っぽいですが 通常の議論の展開ではないです 温度が気体分子1個の平均運動エネルギーを用いて定義されていて それを基にして解いていきます 内部




内部エネルギーと温度 高校物理をあきらめる前に 高校物理をあきらめる前に




気体の分子運動論 高校物理をあきらめる前に 高校物理をあきらめる前に
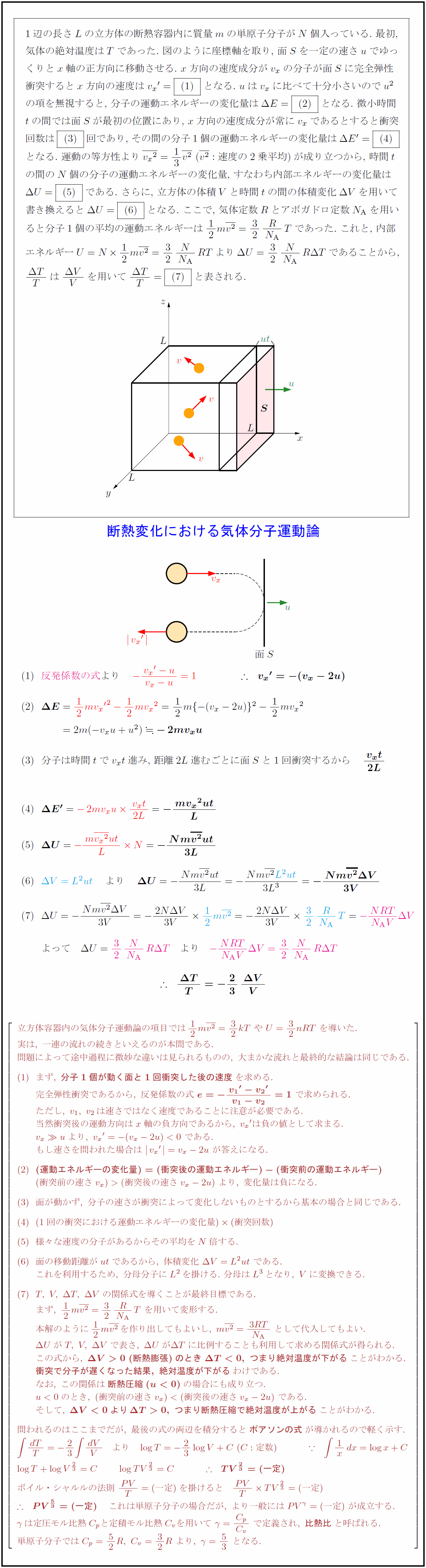



高校物理 断熱変化における気体分子運動論とポアソンの式の導出 受験の月
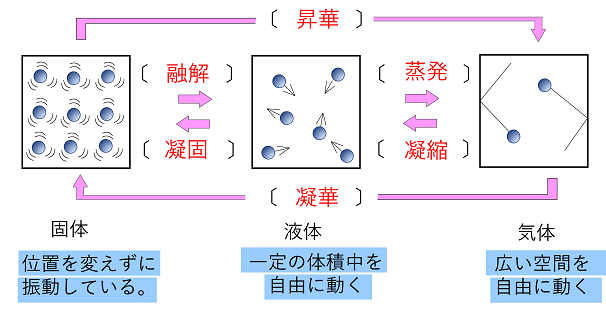



物質の三態と熱運動



温度と熱の伝達



気体分子の熱運動はこのようなグラフになると教わったのですが なぜ同じ Yahoo 知恵袋



1
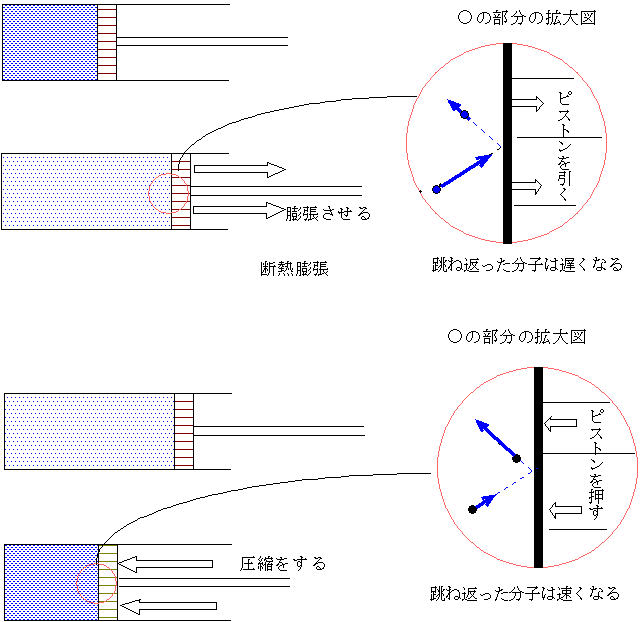



空気の上昇と雲の発生



温度とは
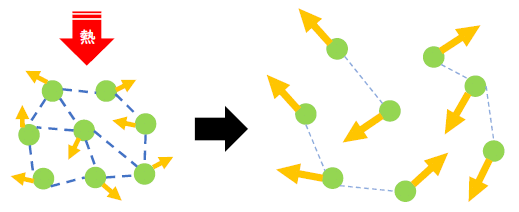



熱の実験室 新館 第48回 粘度が変わる いろんなものを加熱してみた




高校物理 分子運動の等方性 映像授業のtry It トライイット




気体の分子運動論 高校物理をあきらめる前に 高校物理をあきらめる前に



音速の理論2 分子速度と比熱比




高等学校物理 物理ii 熱力学 Wikibooks




高校物理 温度と熱運動 Youtube




気体の分子運動論 高校物理をあきらめる前に 高校物理をあきらめる前に




薬剤師国家試験 医師国家試験 臨床 Ar Twitter マクスウェル ボルツマン分布 同じ温度でも気体分子のもつ分子運動エネルギーや速さにはバラツキがあります 図は 化学の基本ノート より Http T Co Dv5t0blwo8



0 件のコメント:
コメントを投稿